Great Circles!

No, I'm not over-excited about a shape... Great Circles are a 'geographic concept' (via The Map Room).

A great circle is defined as any circle drawn on a globe (or other sphere) with a center that includes the center of the globe. Thus, a great circle divides the globe into two equal halves.

The post reminded me that some additional work on Geoquery 2008 is long overdue. Until then, it prompted me to blog my 'great circle drawing algorithm' as used in Geoquery 2008 to draw lines like this (a 'straight line' between two points, which looks curved on a Mercator projection but is clearly straight when viewed from above on a globe):

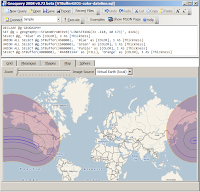
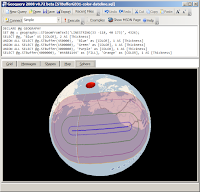
The above example uses SQL Server 2008's STBuffer() geography function - notice how the shaded area looks kidney-shaped on the 'flat' Mercator projection (the curve is more pronounced further north) but on the globe the sides are straight.

You can read the C# code to calculate a Great Circle arc or see it below. Given two System.Windows.Points on a Mercator grid (following the Virtual Earth 'scaling' pattern - notice the hardcoded zoomlevel 2 in the LatLongToPixel method calls) it will calculate a Great Circle between them and plot 10 points along that path (notice the hardcoded 0.1 in the for clause). It returns a System.Windows.Shapes.Polyline ready to draw!


It references Virtual Earth Tile System, and the algorithm itself is based on the work by Ed Williams on Aviation Formulary in particular calculating intermediate points on a great circle.

For those who are really paying attention, you may guess this isn't exactly the code used in Geoquery 2008... for a start 10 divisions was too coarse so Geoquery uses a variable number of points based on the length of the line and its proximity to the poles (where the 'curve' is more pronounced). Geoquery ALSO needs to stop/start drawing lines that cross Longitude 180° (so they wrap nicely on Mercator, and join when projected on a globe)... which is done by calculating the intersection of two great circles because SQL Server 2008 couldn't do it (but that's another story...)

P.S. there are some previous posts on the 'straight line' problem that might be an interesting read...